ggplot2 Quick Reference: alpha
Most geoms have an "alpha" parameter. Legal alpha values are any numbers from 0 (transparent) to 1 (opaque). The default alpha value usually is 1.
The alpha can be set to a constant value or it can be mapped via a scale.
Setting to constant value
To set the alpha to a constant value, use the alpha geom parameter (e.g., geom_point(data=d, mapping=aes(x=x, y=y), alpha=0.5) sets the alpha of all points in the layer to 0.5.
Mapping with scale_alpha_continuous
The scale_alpha_continuous scale can be used to map numbers to a range of legal alpha values.

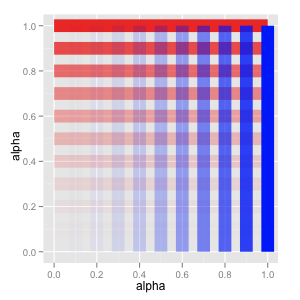
d=data.frame(a=seq(0, 1, 0.1)) ggplot() + scale_alpha_continuous(to=c(0,1), legend=F) + scale_x_continuous(name="alpha") + scale_y_continuous(name="alpha") + geom_segment(data=d, mapping=aes(x=0, y=a, xend=1, yend=a, alpha=a), color="red", size=6) + geom_segment(data=d, mapping=aes(x=a, y=0, xend=a, yend=1, alpha=a), color="blue", size=6)
scale_alpha_continuous(..., to=c(min, max))
The to argument determines the range of alpha values to map to. It represents a vector with two elements, the minimum alpha value and the maximum alpha value to use.
The default range is to=c(0.1, 1), that is, the minimal data value is translated to an alpha value of 0.1 (and thus is not entirely transparent.
In the above example, we explicitly set the range to 0...1 with to=c(0, 1). This, in combination with a transformer that is a linear function with a positive slope (such as the scale's default "identity" transformer), leads to a scale that represents the identity function (a given data value directly represents the alpha).
scale_alpha_continuous(..., trans=...)
The trans argument accepts either a transformer object (of class Trans) or a string representing the name of a predefined transformer object.
If trans is NULL, or the argument is not used, then the default transformer, called "identity" (which passes on the given value; left figure below), is used. Another legal transformer name is "reverse" (which negates the given value; right figure below).


Other, non-linear, transformations exist. One that makes sense for alpha values is "sqrt" (which takes the square root of the given value; left figure below). The inverse, "sqr" (which squares the given value; right figure below), is not available as a built-in transformer.

However, you can easily define your own transformers. Just use Trans$new as follows (here, we define a transformer called "sqr", which squares the given value):
scale_alpha_continuous(to=c(0,1), trans=Trans$new("sqr", function(x) x^2, function(x) sqrt(x), function(x) sqrt(x)), legend=F)
Alternatively, you could subclass Trans:
SqrTrans <- proto(Trans, { new <- function(.) .$proto(objname = "sqr") transform <- function(., values) {if (is.null(values)) return(); values^2} inverse <- function(., values) {if (is.null(values)) return(); sqrt(values)} label <- function(., values) .$inverse(values) })
And then use that subclass:
scale_alpha_continuous(to=c(0,1), trans=SqrTrans$new())


